こんにちは。后稷です。
統計学とは、とあるデータ群を数学的な手法にて分析し、其処に有ると期待される規則性や不規則性の発見を目的とした学問です。統計学の効果的な活用によって、例として、一部分に関する情報を用いての全体像の推測や、過去情報を用いた将来の予測が可能となります。
学問としての統計学は、度数分布の理解を以って其の嚆矢とすべきでありましょう。度数分布の理解は、統計学の学習には欠かせません。本格的な統計学の学習の準備として、以下の動画にて、日常生活の中で見られる出来事や現象の分布に関してお話ししました。
第1章の目次
・実際の統計データを確認
・相対度数曲線の形状
・本日の終わりに
実際の統計データを確認
まずは肥満率の分布です。このデータは、厚生労働省が実施する国民健康・栄養調査(2012)にある第14表を基にしています。なお実線は各階級の発生確率を示す相対度数、点線は其の累計値である累積相対度数です。
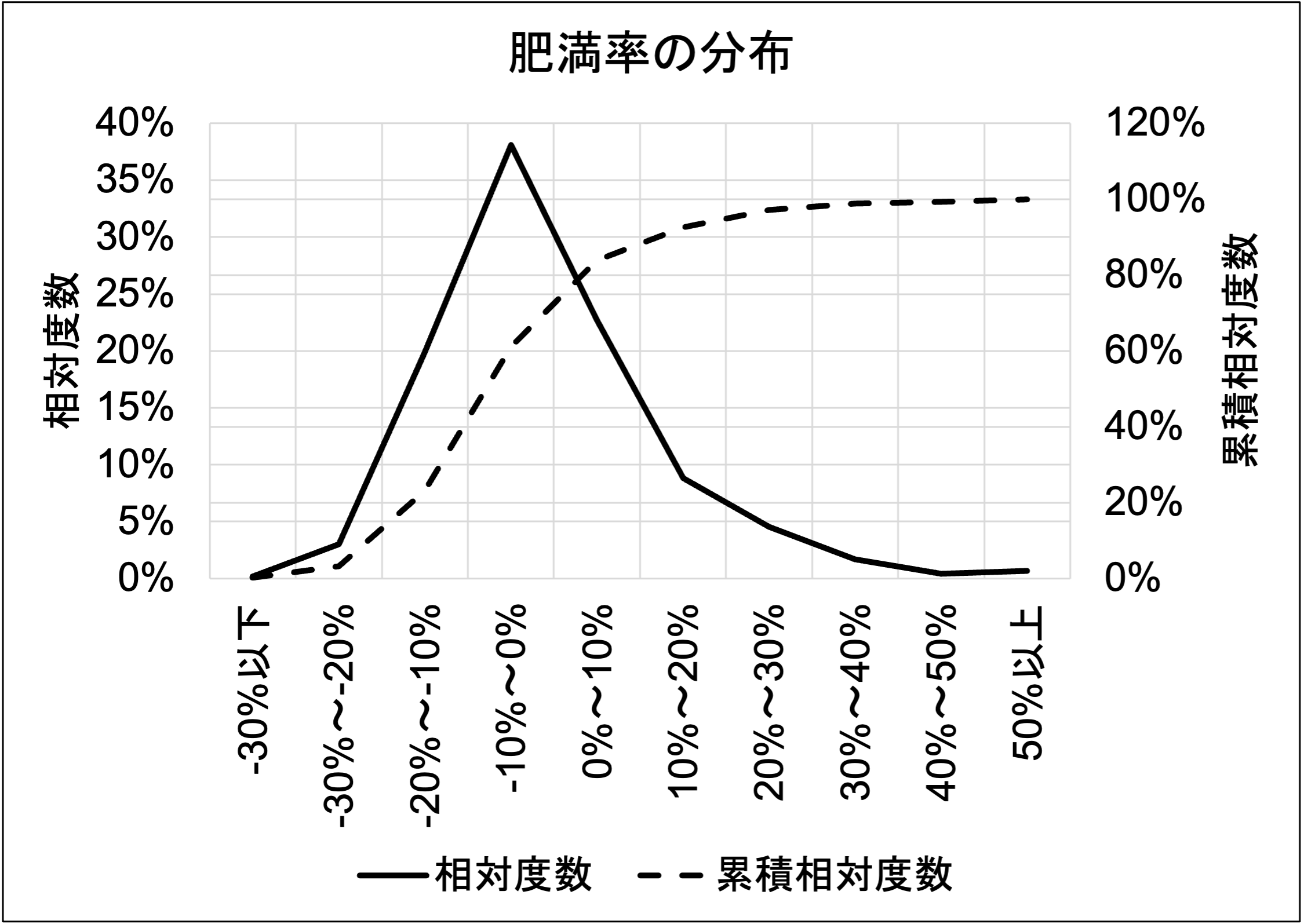
続いては最高血圧の分布です。このデータは、厚生労働省が実施する国民健康・栄養調査(2012)にある参考1の1を基にしています。
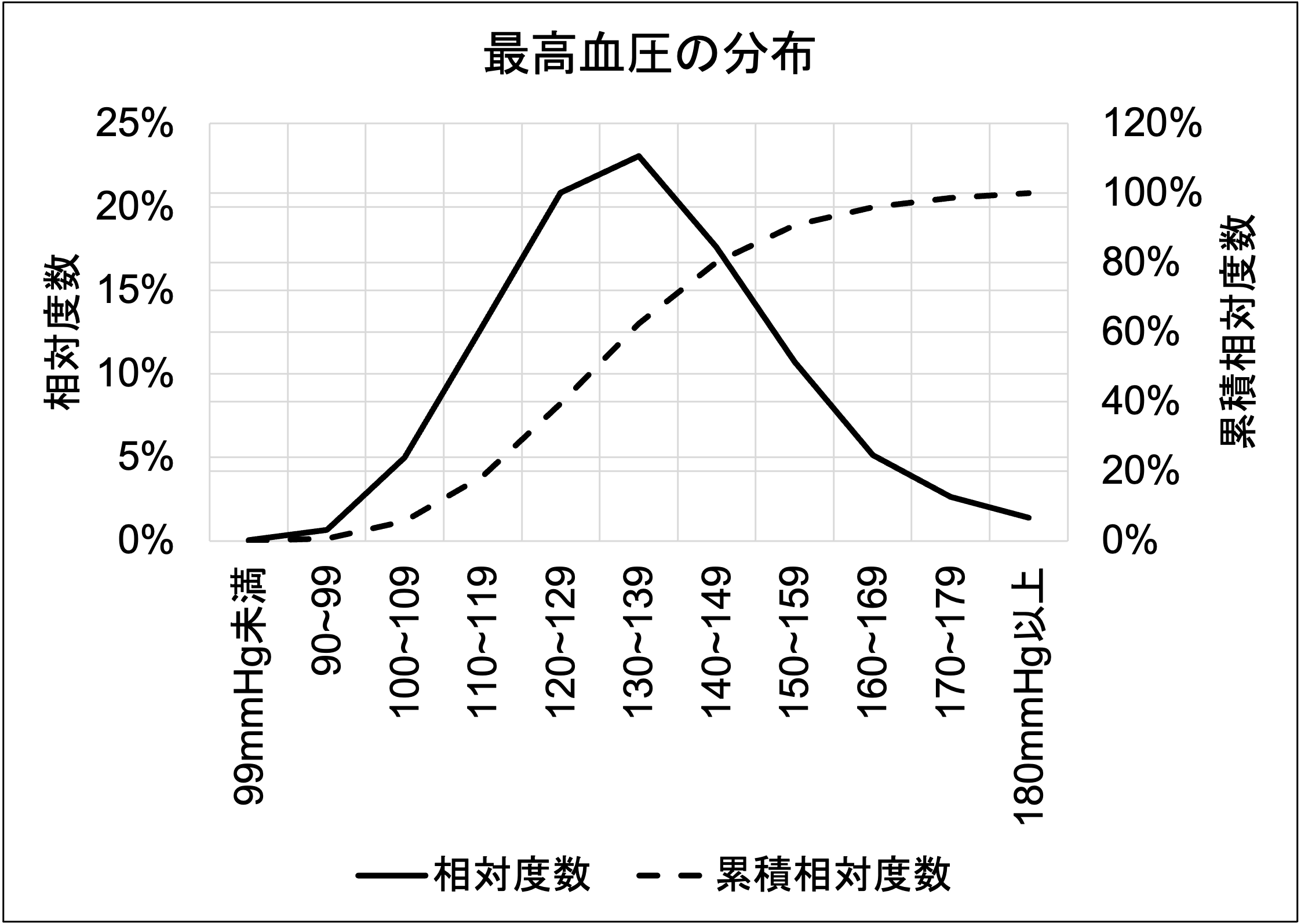
次は所得金額の分布です。このデータは、厚生労働省が実施する国民生活基礎調査(2021年)にある図9を基にしています。なお平均値は564万円、中央値は440万円と報告されています。
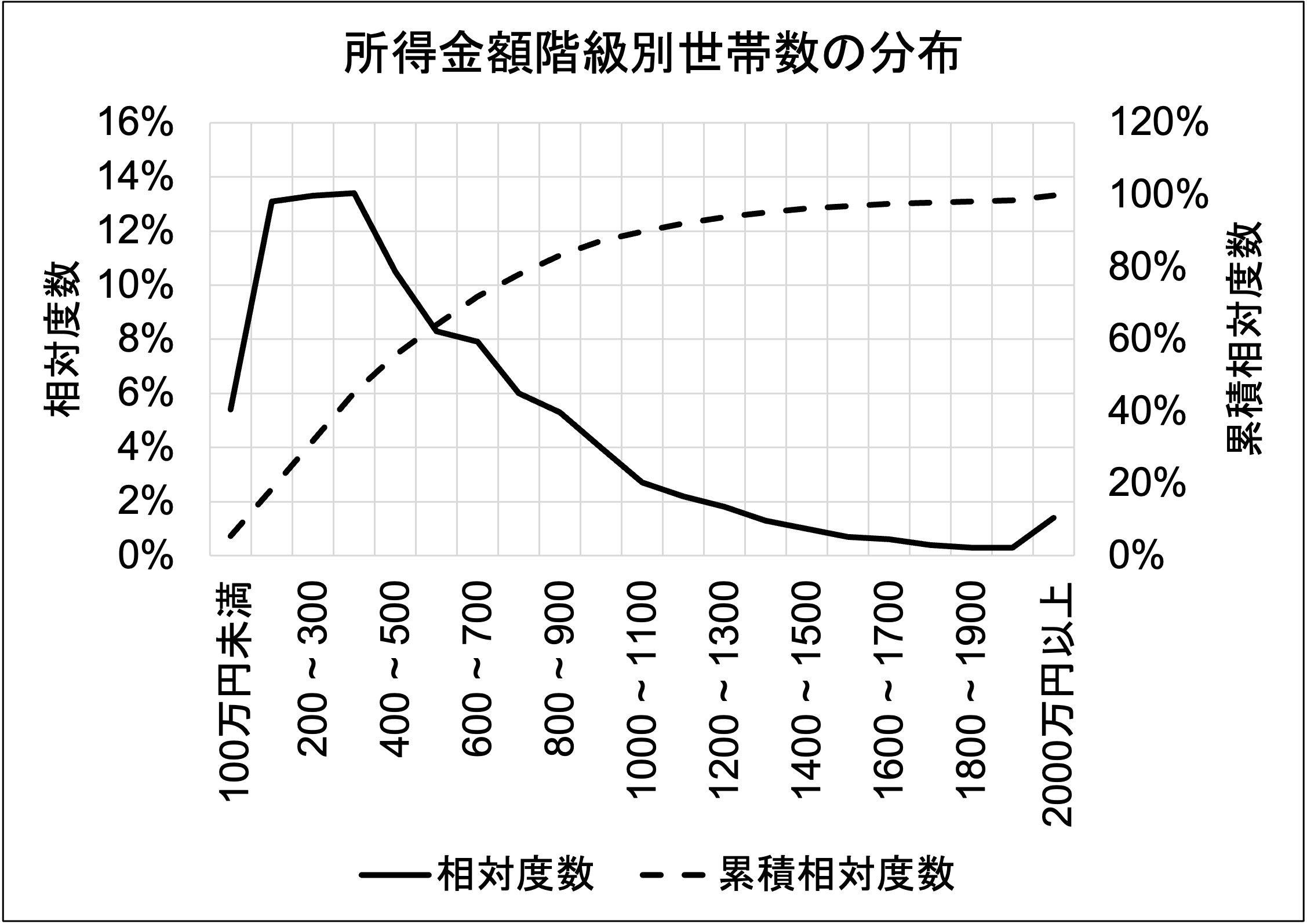
そして最後に、米国株式市場における月間利益率の分布です。該当する期間は1900年1月から2023年1月までの1,477ヶ月間です。なおこのデータは、www.officialdata.orgに記載されているSP500株価指数を基にしています。なお蛇足ですが、当該期間における月間利益率の算術平均値は0.87%でした。
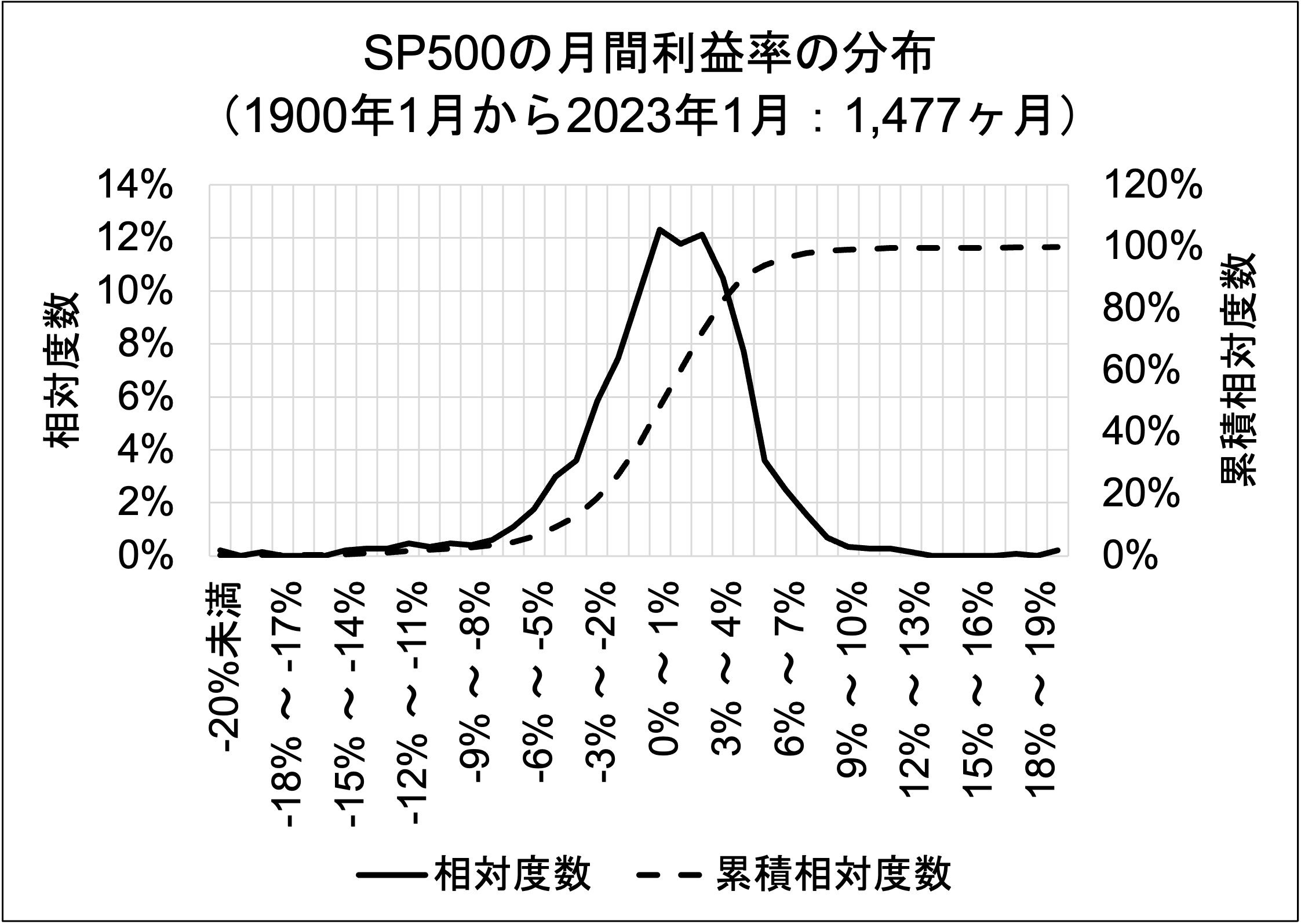
肥満率、最高血圧、所得、そして株式利益率に関する四つの分布を確認しました。これら全てにおいて、相対度数曲線は、多少の個体差はあれど、概ね左右対称の凸型の形状をしています。
極端に小さな数値や大きな数値の発生確率は低く、其の中間付近にある数値の発生確率は高い。平均的な個体は多く、平均から離れた個体は少ない。これは其の他の多くの出来事や事象においても見られる現象です。
相対度数曲線の形状
相対度数曲線の形状には個体差があります。背の高い分布もあれば、背の低い分布もあります。左右の何方か片方に傾いた分布もある。また複数の峰を持つ分布もあります。其の形状は千差万別です。
様々な凸型の形状をした分布の中で、次の四つの条件を満たす分布は、正規分布と呼ばれています。そして世の中で発生する多くの出来事や事象は、正規分布に従うことが知られています。
正規分布の条件
1. 中央部分に山頂が一つ
2. 裾野が左右に長い
3. 左右対称
4. 尖度がゼロ(条件4の影は薄い。後述)
これらの条件が満たされている分布、即ち正規分布は、打楽器であるベルに似た其の形状から、ベル曲線(ベルカーブ)の名で膾炙されています。この形状は決して偶然ではありません。身の回りにある事象に関する分布にて曲線を描画すれば、往々にして、ベル曲線が描かれるでありましょう。

先程に見た四つの分布を、正規分布の観点から、改めて確認します。




肥満率(左上)と最高血圧(右上)の分布は、正規分布の4条件を概ね満たしています。よってこれらは正規分布であると言えます。
一方で、株式月間利益率(右下)の分布は、中心が高い、左右に裾野が長い、左右対称、の3条件は満たしていますが、4番目の条件である尖度ゼロが満たされていません。よって当該分布は、ベル型の曲線を描いてはいますが、厳密には正規分布とは言えません。しかしながら、4番目の条件である尖度ゼロは、世間一般的には余り重要視されていません。よってこのような形状の分布を広義の正規分布と表現しても、特段に問題は無いと思われます。なお尖度に関しては、第二章にてお話し致します。
また総所得(左下)の分布は、右方向に非常に長い裾野を持っています。左方向の裾野が短いために、当該分布の形状は左右対称ではありません。よって正規分布の条件を満たしていません。このような形状は、対数正規分布、カイ2乗分布、F分布などではよく見られます。これら特殊な分布に関しては、学習が進んで後に、日を改めてお話し致します。
本日の終わりに
第1章である本日は、度数分布に関してお話し致しました。そして身の回りにある出来事や事象の代表例として、四つの分布がベルに似た凸型の曲線を描く様子を確認しました。この曲線は、人々の身長や体重、経済成長率、数学の試験の点数、などなど、様々な場面で見られる現象です。もし機会があれば、興味を惹かれる分野の分布を調べるのも面白いかも知れません。
第2章では、統計学を学ぶに際して必須とも言える、基礎的な統計用語に関してお話しします。お目汚し失礼致しました。近い将来に、またお逢いできたら幸いです。
怱々不一
有栖川后稷
