こんにちは。后稷です。
データを詳しく分析し、其処に存在するであろう規則性を発見・活用するためには、統計学における基礎とも言える統計量(個別データの特徴を要約した数値)の知識が欠かせません。基礎がしっかり固まって居なければ、基礎の上に建つ応用を理解することはできません。多少の回り道にはなりますが、足元にある基礎を確実に身に付ける姿勢は有意義です。
第二章である今回は、より高度な学習へ向けての準備として、基礎的な統計量を扱っています。各統計量の意味、計算に必要な方程式、其れに替わるMS Excelの関数、そして実際に数字を用いての計算例を、以下の動画にて、簡潔にお話し致しました。
第2章の目次
・確率変数
・基本統計量(代表値)
・平均値
・中央値
・最頻値
・基本統計量(散布度)
・範囲
・分散
・標準偏差
・変動係数
・歪度
・尖度
・外れ値
・相対度数分布への影響
・本日の終わりに
確率変数
其の卑近な例としては、賽の目、コインの裏表、新生児の性別、往来ですれ違う人々の身長、明日の気温や日経平均株価の値動き、などが挙げられます。これらを総称して、確率変数と呼びます。
確率変数とは、無作為かつ不規則に、乱歩・酔歩にて発生する出来事や事象の結果を示す文字記号です。漢字より横文字の方が、其の意味はより解り易いかも知れません。確率変数は英語でRandom Variableと言います。Randomの和訳は、無作為、不規則、予測不能などです。Variableは変動可能、未決定、不安定などです。よって確率変数は、次に何が来るか事前には予測できない物事、と言えます。
確率変数は、結果の種類数に応じて、離散型と連続型に大別されます。
離散型である確率変数
出来事や事象の結果数が加算的であれば、当該事象に関する確率変数は離散型です。加算的とは、全てを数えられる、の意味であり、結果の数が有限である様子を示します。有限、即ち限りが有るので、其の全てを数え上げることが可能です。
離散型である確率変数の代表例としては、賽の目やコインの裏表などが挙げられましょう。前者の結果は1から6までの6通りであり、後者は裏か表かの2通りです。其の何方も、結果の数は有限です。
以下の図表は、離散型確率変数の一例として、賽の目の発生確率を示します。

通常のサイコロでは、賽の目は1から6までの6通りです。賽の目が特定の値となる確率は、六つの選択肢の中から一つが選ばれるので、それぞれ1/6となります。また発生確率は、特定の値に替えて、特定の範囲としても算出されます。離散型の確率変数においては、特定の範囲の発生確率は、単純な足し算で計算されます。
連続型である確率変数
出来事や事象の結果数が非加算的であれば、当該事象に関する確率変数は連続型です。非加算的とは、全てを数えられない、の意味であり、結果の数が無限(∞)である様子を示します。無限、即ち限りが無いので、其の全てを数え切ることは不可能です。
連続型である確率変数の代表例としては、人々の身長や体重などが挙げられます。これらには無限の結果があります。小数点の数は無限に続き得るので、身長や体重の結果数は無限です。
以下の図表は、連続型確率変数の一例として、人の身長の発生確率を示します。

身長は必ずしも正の整数とは限らず、また小数点は無限に続き得るので、身長には∞通りの結果があります。よって特定の値の発生確率は1/∞となり、其の値はゼロに近似します。例えば身長が170cm丁度の確率はゼロです。連続型確率変数における発生確率は、特定の値に替えて、特定の範囲として計算する必要があります。其の計算には、微分積分学における積分法を用います。
基本統計量(代表値)
複数のデータが数多く存在する場合には、それら個々の情報を個別に管理し分析を行うと、非常に多くの時間と労力を要してしまいます。分析の苦労と、分析結果の精度は、必ずしも、比例しません。より効率的、かつ効果的な分析を行うために、複数のデータを一つの値、即ち代表値に収斂する配慮は有意義です。
代表値は、全ての情報の中心部付近に位置する値です。物事の中心的傾向を示し、全体をよく代表すると期待されます。其の計算は非常に容易なので、世間一般的に広く利用されていると思われます。
代表値としては、主に、次の三つが挙げられます。其れ等は、平均値、中央値、そして最頻値です。
平均値
平均値は、全個別データの中心部付近に位置し、全体を良く代表する数値です。個々のデータが持つ特性を一つの数値に収斂することで、より効率的かつ効果的な情報の管理が可能となります。
一言で平均値と言っても、其の用途に応じて、様々な種類があります。比較的によく知られている平均値として、算術平均、幾何平均、加重平均、調和平均、加重調和平均、対数平均、などが挙げられます。データの管理を行う者は、自身の目的に相応しい種類の平均値を適宜に選択する配慮が求められます。
これら平均値のうちで、最も基礎的だと思われる算術平均と幾何平均についてお話しします。
算術平均値
算術平均は、最も基礎的かつ最初に学ぶべき平均値だと思われます。日常生活において単に平均値と言えば、多くの場合において、其れは算術平均でありましょう。なお算術平均は、別名として、単純平均や相加平均とも呼ばれます。
算術平均は、全ての確率変数Xを平等に扱い、全体の差異を平らに均した数値です。其の方程式は次の通りです。
\(算術平均値=\mathrm{\frac{\displaystyle\sum_{i=1}^{n}x_{i}}{n}}\)
MS社の表計算ソフトExcelでは、関数AVERAGE(範囲指定)にて計算されます。なお英単語AVERAGEの和訳は平均値です。
幾何平均値
幾何平均は、主として、長期投資家が平均利益率を計算する際に用いられます。長期投資においては、投資期間中に発生する投資利益は、更なる利益を獲得すべく、投資元本に組み込まれます。こうして利益の上に利益が発生する仕組み、複利の原理、が実現します。幾何平均は複利の効果を考慮します。別名として、相乗平均と呼ばれることもあります。
幾何平均値は、先ほどの算術平均と同様に、全ての確率変数Xを平等に扱います。其の方程式は次の通りです。
\(幾何平均値=\mathrm{\sqrt[n]{\displaystyle\prod_{i=1}^{n}x_{i}}}\)
MS Excelでは、関数GEOMEAN(範囲指定)にて計算されます。なお幾何平均の和訳はGeometric Meanです。
中央値
中央値は、先に見た平均値と同様に、数多く存在するデータの中心部分に位置する数値です。しかし平均値とは異なり、中心部から離れた処にある数値を計算から除外する効果があります。
中央値は、確率変数Xを大きい順(小さい順でも可)に並べた時に、順位が全体の中央に位置する値を指します。中央に一つの数値があれば其の数値が、中央に二つの数値があれば其の算術平均が、それぞれ中央値となります。其の方程式は次の通りです。上の方程式は確率変数Xの個数nが偶数の場合、下は奇数の場合となります。
\(中央値=\mathrm{\displaystyle\frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2}}\)
\(中央値=\mathrm{x_\frac{n+1}{2}}\)
MS Excelでは、関数MEDIAN(範囲指定)にて計算されます。なお英単語MEDIANの和訳は中央値です。
最頻値
最頻値は、出現の頻度・回数が最も多い値を指します。発生確率が最も高い確率変数Xを知るのに便利です。凸型である相対度数分布における山頂部分が最頻値です。左右に長く伸びる裾野は、最頻値には全く影響を与えません。
最頻値には特別な方程式は存在しません。全ての確率変数Xを目視し、最も発生回数の多い数値を特定します。MS Excelでは、関数MODE(範囲指定)で計算されます。なお英単語MODEの和訳は流行や様式です。
基本統計量(散布度)
もう一つの基本統計量である、散布度についてお話しします。
代表値の件で触れた様に、複数のデータが数多く存在する場合には、其れ等の中心部付近に位置する代表値を利用することで、より効率的な分析が可能となります。しかしながら、代表値はあくまで、各個別情報の中心的傾向を示す数値に過ぎないので、代表値を見ただけでは、集団全体に関する正確な状況判断は叶いません。より正確な分析を行う為には、個別情報の散らばり具合に関する理解は欠かせません。
散布度は、各個体の格差を要約した値です。物事の散らばり具合や、乖離状況を知るのに便利です。其の計算は、やや煩雑なので、代表値ほどには、世間一般で広く利用されてはいない様に思われます。
散布度としては、主として、次の六つが挙げられます。其れ等は、範囲、分散、標準偏差、変動係数、歪度、そして尖度です。
範囲
範囲とは、確率変数Xが発生する幅を示します。確率変数Xが狭い範囲に集中的に発生すると幅の値は小さく、広い範囲に拡散的に発生すると幅の値は大きくなります。範囲はデータの散らばり具合を簡易的に示します。
範囲は最大値と最小値の差異として計算します。両極端の数値のみから算出されるので、確率変数Xに異常な数値が混在していると、範囲は当該異常値の影響を強く受けてしまいます。MS Excelでは、最大値は関数MAX(範囲指定)、最小値は関数MIN(範囲指定)にて、それぞれ計算されます。なおMAX及びMINは、それぞれMaximumとMinimumの略語であり、其の和訳は最大と最小です。
分散
分散は、確率変数Xが平均値から乖離する度合いを示します。小さい分散は確率変数Xが平均値に近い処にて集中的に発生する様子を示します。反対に、大きい分散は、確率変数Xが平均値から遠く離れた処で散らばって発生する様子を示します。
先に示した範囲も、分散と同様に、確率変数Xの散らばり具合を示す指数ではあります。しかし範囲が最大値と最小値という両極端の二点しか考慮しないのに対し、分散は全ての確率変数Xを平等に考慮します。よって分散は、範囲より、遥かに精度の高い指数となります。其の方程式は以下の通りです。
\(分散=\mathrm{\frac{\displaystyle\sum_{i=1}^{n}(x_{i}-算平)^2}{n}}\)
MS Excelでは、関数VAR.P(範囲指定)にて計算されます。なおVAR及びPは英単語VarianceとPopulationの略語であり、其の意味は分散と母集団(全体)です。
標準偏差
標準偏差は、先に見た分散と同様に、確率変数Xが平均値から乖離する度合いを示します。其の値は分散の平方根と一致します。分散は計算の過程で二乗されています。よって二乗される前の状態である確率変数Xとは、対等の立場で、並べて比較はできません。この問題は標準偏差の利用によって解決します。こうして平均値や確率変数Xと標準偏差の足し算や引き算などの計算が可能となります。
標準偏差の方程式は以下の通りです。なおルート内は分散の方程式と同一です。
\(標準偏差=\mathrm{\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-算平)^2}{n}}}\)
MS Excelでは、関数STDEV.P(範囲指定)にて計算されます。なおSTDEV及びPは英単語Standard DeviationとPopulationの略語であり、其の和訳は標準偏差と母集団(全体)です。
変動係数
変動係数は、分散や標準偏差と同様に、確率変数が、平均値から乖離する度合いを示します。とある集団の散らばり具合を、他の集団の其れと比較する際に、変動係数は有意義です。
分散及び標準偏差は、各Xと平均値との差異を基に計算されます。よって、複数の集団が、それぞれ異なる平均値を持つ場合には、集団間での、分散や標準偏差の比較は無意味です。其の為、これら数値は、散らばり具合に関する、絶対評価の指数と言えます。他者との比較には、やや使い辛いと思われます。
この問題は、変動係数の利用により、解決します。変動係数は、平均値が異なる集団間における、散らばり具合の比較に用いられます。其の性質から、変動係数は、相対的標準偏差と呼ばれることもあります。
方程式は、この通りです。
\(変動係数=\displaystyle\frac{標準偏差}{算術平均}\)
分子の標準偏差と、分母の算術平均は、共に同じ単位を持っています。例えば、体重ならば、キログラムやポンドなどの、重量の単位、お金ならば、日本円やアメリカドルなどの、通貨の単位、という様に、分子と分母の単位は、共通しています。これら単位は、分数の約分により、消えて無くなります。これにより、単位の異なる集団間や、平均値が異なる集団間での、散らばり具合の比較が可能となります。
MS Excelには、変動係数に該当する関数は、備わっておりません。よって、先に見た、算術平均と標準偏差の関数を、組み合わせて計算されます。
歪度(わいど)
歪度は、多くの人にとって、聞き慣れない用語でしょうか。歪む(ゆがむ・ひずむ)度合いと書いて歪度と読みます。歪度とは、其の名が示す通りに、分布の左右対称性が歪む度合いを示します。分布が左右対称ならば、歪度はゼロとなります。正の歪度は相対度数分布の裾野が右方向に、負の歪度は裾野が左方向に、それぞれ長く伸びている状況を示します。
確率を論じるに際しては、分布が左右対称であるとの前提が敷かれる場合は多い。よって歪度は最初に確認したい指数ではあります。其の方程式は以下の通りです。
\(歪度=\displaystyle\mathrm{\frac{\frac{\displaystyle\sum_{i=1}^{n}(x_{i}-算平)^3}{n}}{標偏^3}}\)
MS Excelでは、関数SKEW.P(範囲指定)にて計算されます。なおSKEWは英単語Skewnessの略語であり、其の意味は歪度です。またPはPopulation、母集団(全体)です。
尖度(せんど)
先の歪度と同様に、尖度もまた、馴染みの薄い単語だと思われます。尖る(とがる)度合いを書いて尖度と読みます。尖度は相対度数分布の山頂と裾野の形状を示します。正規分布における尖度はゼロと定義されます。尖度が正数の分布は、山頂が細く高く、裾野が太く長くなります。尖度が負数の分布は、山頂が太く低く、裾野が細く短くなります。
尖度ゼロは正規分布の条件の4番目に挙げられてます。しかし世間一般的には、尖度は然程には注目されていません。たとえ尖度がゼロでなくても、其の他の3条件が満たされる分布は、広義の正規分布と考えても特段に問題はないと思われます。尖度の方程式は以下の通りです。
\(尖度=\displaystyle\mathrm{\frac{\frac{\displaystyle\sum_{i=1}^{n}(x_{i}-算平)^4}{n}}{標偏^4}-3}\)
MS Excelには、尖度に該当する母集団用の関数は備わっておりません。試査用である関数KURT(範囲指定)のみの搭載となります。なおKURTは英単語Kurtosisの略語であり、其の和訳は尖度です。
外れ値
最後に採り上げるは外れ値です。外れ値とは、其の名が示す通りに、其の他の多くの情報から遠く離れた処で発生する異質な数値です。これまでは、中心部から離れた処にある数値、などと表現して参りました。これら珍しい個体は、統計用語では、外れ値と呼ばれます。
集計したデータに外れ値が混在していると、全体の平均値や標準偏差などの統計量が大きく歪んでしまう場合があります。外れ値では、其の特異性から、全体像を適切に示す一般論を導き出すことができません。より有意義な分析を行うために、外れ値を適宜に除外する配慮が求められます。
なお中央値は、大きい順に並べた際の両極端にある個体を計算から除外する性質から、外れ値の影響を殆ど受けません。
また外れ値は、珍しい個体の意味から、黒い白鳥(Black Swan)と表現されることもあります。アメリカの作家かつ数学者であるナシーム・タレブ氏の著書「The Black Swan」は有名です。
相対度数分布への影響
分布の形状には様々な種類があります。形の整った左右対称の分布もあれば、裾野が何方か片方に長く伸びた分布もある。細く高い分布あれば、太く扁平な分布もあります。其の形状は千差万別です。
分布の形状は、先に確認した統計量にて示されます。本節では、これら数値が分布に与える影響についてお話しします。
正規分布においては、平均値は凸型の山頂部分に位置します。平均値が変化すると、凸型の曲線は、形状を維持しながら、左右に動きます。なお正規分布においては、平均値と中央値そして最頻値は必ず一致します。
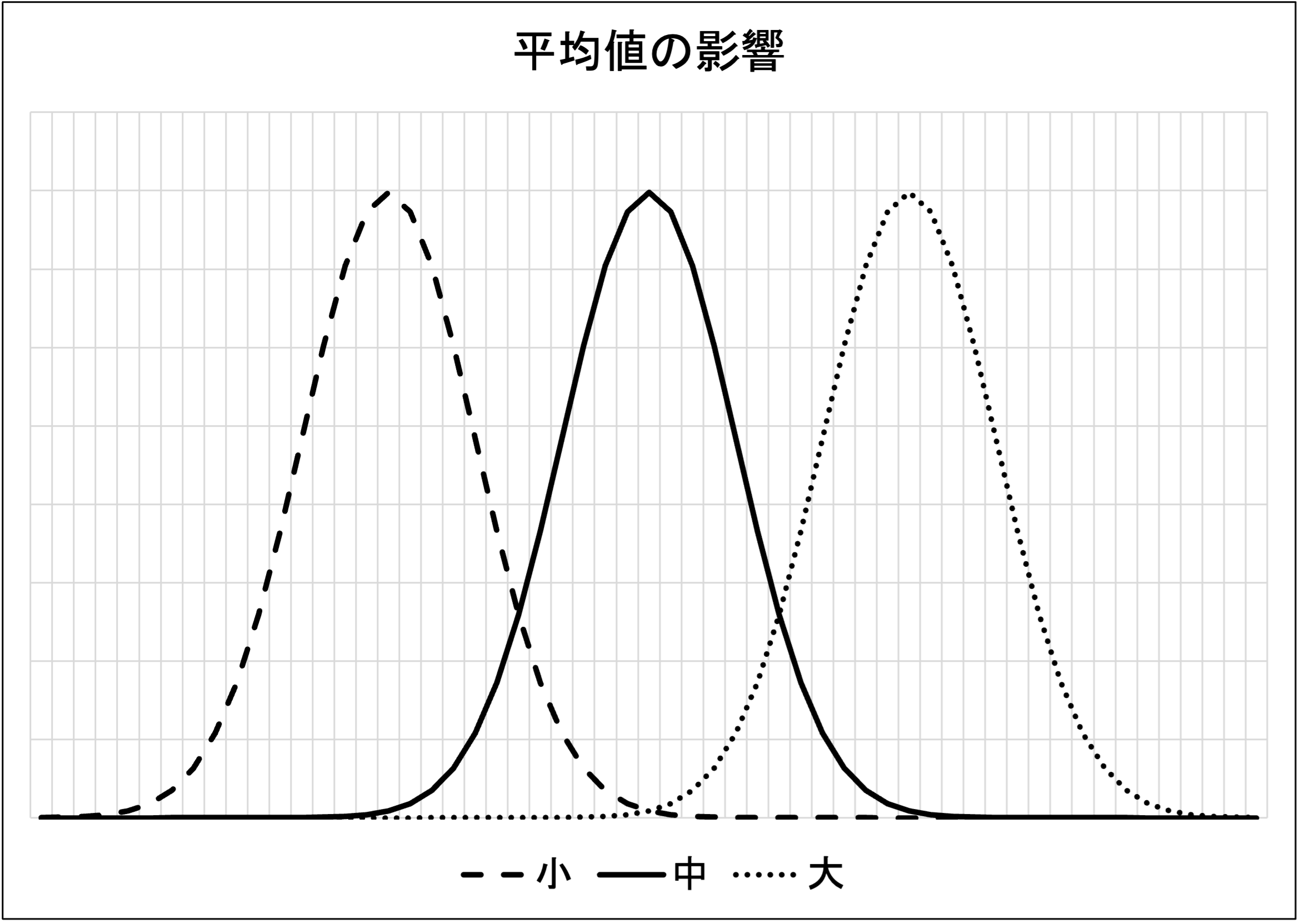
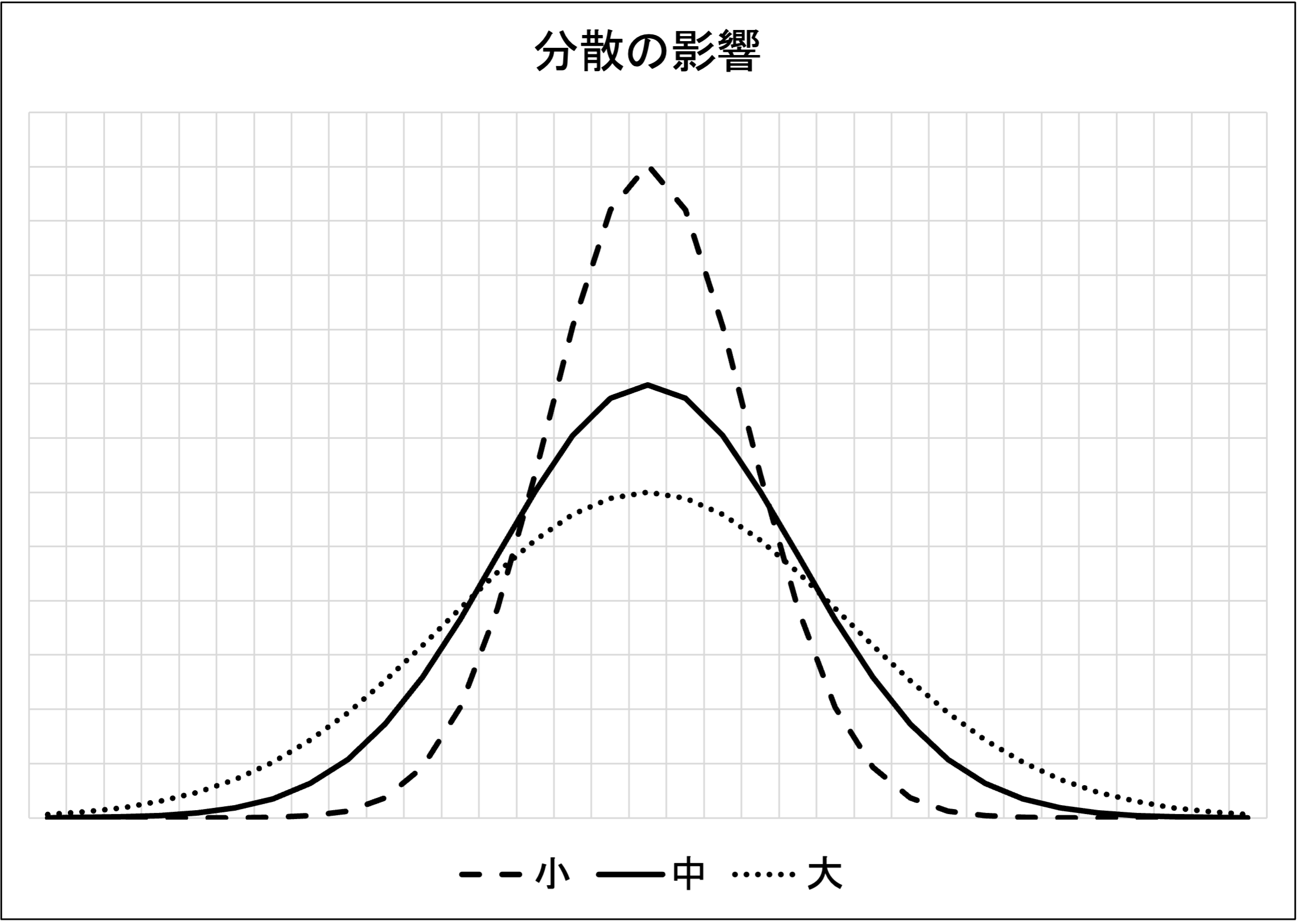
分散(及び其の平方根である標準偏差)が増減すると、分布の凸型は其の形状を変えます。分散が小さくなると、確率変数Xが山頂部分にある平均値に引き寄せられるために、分布の背は高く裾野は短くなります。一方で、分散が大きくなると、確率変数Xが山頂から遠く離れた処で発生するために、凸型の形状は下方向に押し潰された様に、背は低く裾野は長くなります。
正規分布の歪度はゼロです。歪度が正方向に大きくなると、凸型曲線の裾野が右方向に長く伸びます。すると其れまでは一致していた平均値と中央値そして最頻値に乖離が生じます。裾野が右方向に長い分布では、最頻値≦中央値≦平均値となります。また歪度が負方向に大きくなると、左側の裾野が長くなります。すると平均値≦中央値≦最頻値となります。平均値が長い裾野の方向に引き寄せられる現象には要注意です。

なお分布が左右の何かに偏っている場合には、長い裾野がある方向にて其の歪みを示す表現が適切です。しかしながら、裾野より山頂の方が人の目を惹き易いためか、山頂に着目して分布の傾き具合を表現する人が散見されます。其のため意思の疎通が困難になる場合があります。裾野には平均値を歪める力があります。分布の歪みを表現するに際しては、裾野を強調する配慮が求められます。
尖度は山頂と裾野の形状に影響します。高い尖度は、山頂と裾野の両方を厚くします。結果として、山頂と裾野の間にある中間層が薄くなります。一方で低い尖度は、山頂と裾野の両方を薄くします。そして中間層が厚くなります。
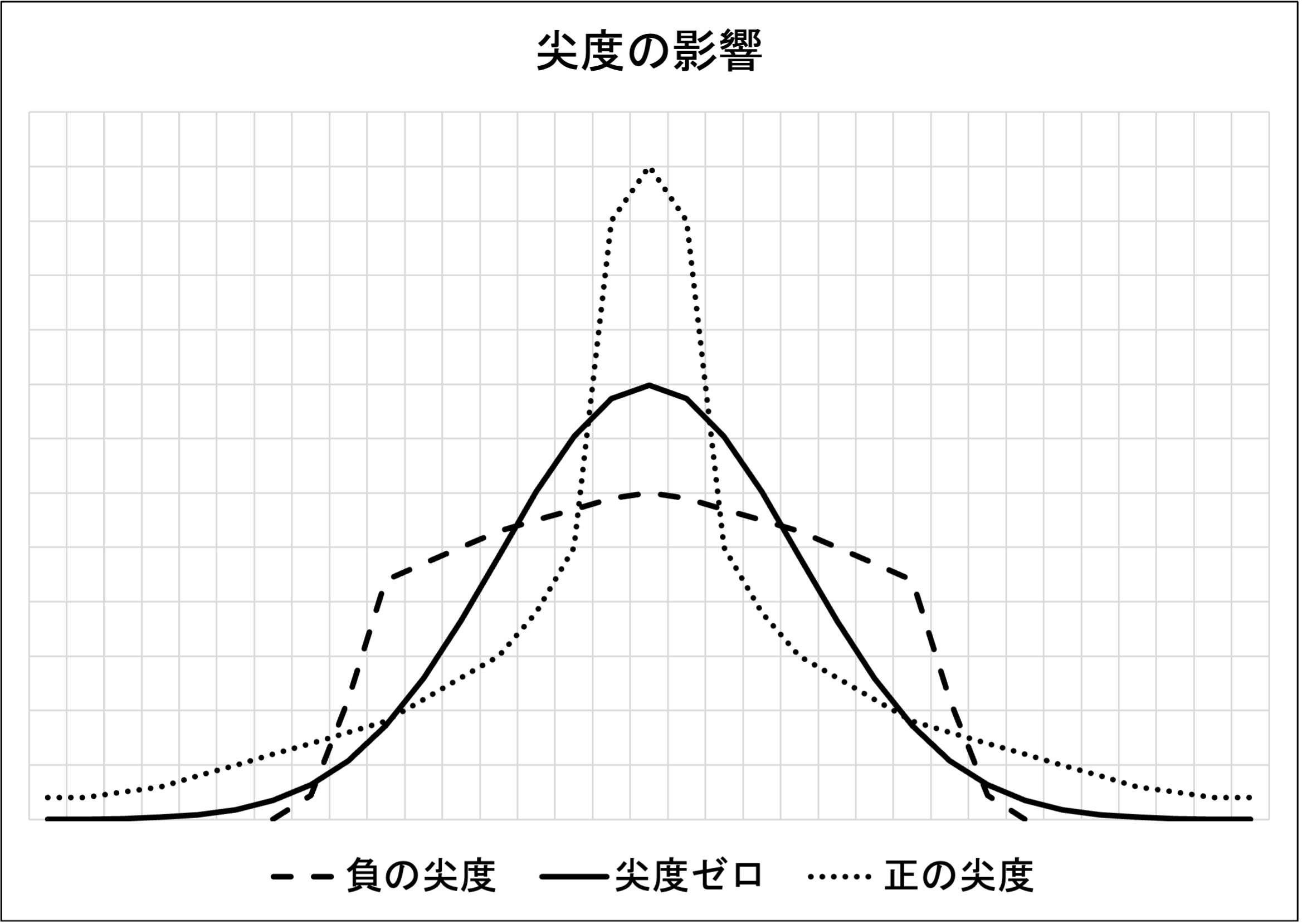
ネット上にて尖度に関する記述及び画像を数点確認しましたが、尖度と分散の影響を混同している様な記述が散見されました。これら二点には類似点があるので、細かい論点ではありますが、やや注意が必要です。
本日の終わりに
本日に確認した10個の統計量は、統計学の基礎中の基礎であり、これら用語を知らずして統計学を正しく学ぶことは出来ません。これから始まる統計学の学習を、より効果的かつ有意義にする為に、これら統計用語には十分に慣れ親しむが賢明です。
第3章では、順列と組合せに関してお話しする予定です。お目汚し失礼致しました。近い将来に、またお逢いできたら幸いです。
怱々不一
有栖川后稷

