こんにちは。后稷です。
複数の選択肢の中から、特定の個体を選択し、抽出する方法には、順列(P)と組合せ(C)の二つがあります。これらは、同一個体の反復した選択が認められる場合には、特に、重複順列や重複組合せと呼ばれています。こうして、全部で四つに区分されます。
洋菓子店にて陳列されている多くの選択肢の中から数個のケーキを購入する際や、競馬場にて馬券を購入する際など、順列や組合せの知識が大いに役に立つと期待される場面は多々あります。日常生活においても有用な順列や組合せの仕組みを、以下の動画にて簡潔に纏めました。
第3章の目次
・全部で四種類
・重複のない組合せ
・重複のない順列
・重複のある組合せ
・重複のある順列
・本日の終わりに
全部で四種類
複数の選択肢から個体を抽出する方法は、重複の有無により、二つに大別されます。また其々に、組合せと順列があります。こうして全部で四つの項目に区分されます。なお重複とは、同じ個体を繰り返し(二回以上)選択するという意味です。
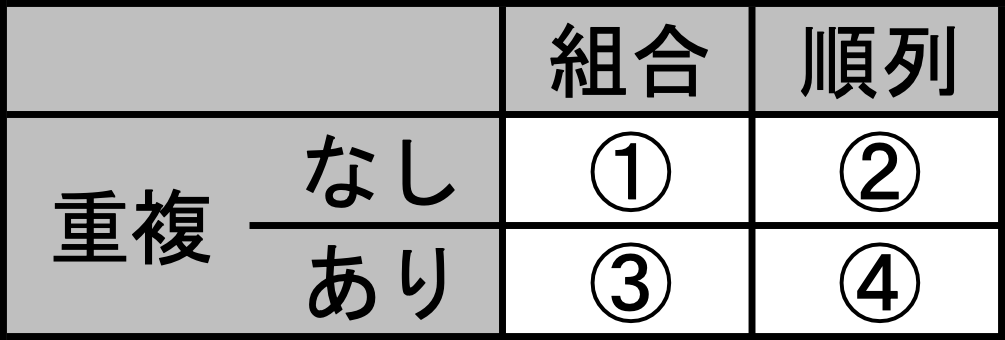
これら四つの内で、二項分布にて用いられる項目は①と③と④の三つです。しかしながら、折角の機会ですので、これら全てについてお話しします。
① 重複のない組合せ
「重複がない」とは、選択肢の中から複数の個体を抽出する際に、同じ個体を繰り返し選択してはならない、の意味です。それぞれの個体が抽出される回数は、最大で1回までです。一度も選ばれない可能性もあります。
また組合せは、個体の抽出に際して、其の順序は問いません。卑近な例としては、ポーカーの役を構成するカードや競馬の三連複が挙げられます。これらは個体の選択のみが重要であり、其の順番は考慮の外に置かれます。
重複のない組合せ数の方程式は、以下の通りです。
重複のない組合せ数 \(={}_nC_r=\displaystyle{\frac{n!}{(n-r)!r!}}\)
なお方程式にあるnは選択肢数、rは抽出数です。また感嘆符(!)は階乗、即ち、1から任意の値までの間にある全ての整数の積、の意味です。またCは、組合せを意味する英単語Combinationの頭文字です。
MS社の表計算ソフトExcelでは、関数COMBIN(選択肢数,抽出数)にて計算されます。COMBINはCombinationの略語であり、其の和訳は組合せ・連結です。
② 重複のない順列
先に見た①重複のない組合せと同様に、重複のない順列もまた、それぞれの個体が抽出される回数は1回までです。繰り返し選択されることはありません。
また順列は、個体の抽出に際して、其の順序が重要となります。身近な例としては、学校や職場での席順や競馬の三連単が挙げられます。これらにおいては、個体の選択のみならず、其の順序もまた重要となります。
重複のない順列数に関する方程式は、以下の通りです。
重複のない順列数 \(={}_nP_r=\displaystyle{\frac{n!}{(n-r)!}}\)
MS社の表計算ソフトExcelでは、関数PERMUT(選択肢数,抽出数)にて計算されます。PERMUTは英単語Permutationの略語であり、其の和訳は順列・並べ方です。
③ 重複のある組合せ
重複があるとは、選択肢の中から複数の個体を抽出するに際して、同一の個体を繰り返し選択しても良い、との意味です。各個体は何度でも抽出できます。
また組合せなので、個体の抽出の順序や並べ方は考慮しません。身近な例としては、オンラインショップでの買い物やカクテルの作り方などが挙げられましょう。これらは同一の選択肢を選び続けても良く、また其の順番は問われません。
重複のある組合せ数の方程式は、以下の通りです。
重複のある組合せ数 \(={}_{n+r-1}C_r=\displaystyle{\frac{(n+r-1)!}{(n-r)!r!}}\)
なお重複のある組合せ数の方程式としては、nHrと表現される場合もあります。しかし当該表記は日本独自なので、可能な限り、使用は控えるが賢明です。
MS社の表計算ソフトExcelでは、関数COMBINA(選択肢数,抽出数)にて計算されます。COMBINAは英単語Combinationの略語であり、其の和訳は組合せ・連結です。
④ 重複のある順列
同じ個体を繰り返し抽出でき、また並び順を考慮する時に、其の選択は重複のある順列となります。日常生活で馴染み深い重複のある順列としては、銀行の口座番号や金庫の暗証番号などが挙げられます。
重複のある順列数の方程式は、以下の通りです。
重複のある順列数 \(=n^r\)
なお重複のある順列数の方程式としては、nΠrとの表現も散見されます。しかし当該表現は日本独自なので、可能な限り、使用は控えるが良いでしょう。
MS社の表計算ソフトExcelでは、関数PERMUTATIONA(選択肢数,抽出数)にて計算されます。PERMUTATIONAは英単語Permutationalの意であり、其の和訳は順列・並べ方の形容詞です。
本日の終わりに
順列や組合せに関する知識は、日常生活の様々な場面にて、我々の意思決定を然りげ無く支援してくれると期待されます。また順列及び組合せの知識なくして、正確な確率の計算は叶いません。方程式を丸暗記する必要はありませんが、CとPの違いはしっかりと理解しておきたい処ではあります。
第4章では、ベルヌーイ分布及び二項分布についてお話しする予定です。これまでは基本的な事柄のみを扱って参りましたが、いよいよ次回から、本格的に統計学らしい内容となります。お目汚し失礼致しました。近い将来に、またお逢いできたら幸いです。
怱々不一
有栖川后稷

